With a bit of effort tracking which loops are inside others, you can map the loop and subloop relationship to graph and subgraph keywords in DOT. Here's the code, here's some screenshots from busybox:

I was wrong in my last post about there not being a worthy python implementation of loop detection we could compare our results against. It's in miasm.

Thank you to them for a clear, straightforward API, with straightforward named functions like compute_natural_loops().

The test is updated now and thankfully binja and miasm are in agreement for loops in busybox x86_64.

recap: - A boolean attribute is being added to basic blocks to reflect the block's membership in a loop. - I need something to compare the algorithm's results to, but I can't find a turn-key (ie: available in PyPI) library with natural loop detection. - NetworkX is a graph theory library that seems established and tested. - Porting the algorithm to NetworkX and comparing outputs for many inputs would reveal errors in areas the algorithm relies on, like calculation of dominators, but would mask errors in the algorithm itself. - The algorithm's simplicity and its established pedigree does not exempt our implementation from suspicion. Errors have already been found when processing a self-branching block and another based on an ambiguity in the definition of back edge. See this revision history. - Therefore, I want to compare the algorithm to one with an intentionally different approach.

Alternative approach:

A block is in a loop when it is in a cycle and at least one edge B -> A in the cycle has A dominating B.

A program loop is like a cycle in a graph. And the requirement of A dominating B means A necessarily executed before B, so B -> A is "returning" to A, a back edge. So it must be equivalent, right? Yes, 99% of the time. To my complete surprise, a giant function in busybox was a counterexample. Red blocks are identified by the standard algorithm but not the alternative. Here's an attempt at minimizing it:

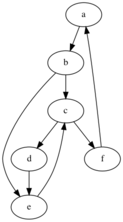
Compare the behavior of the two algorithms.

standard algorithm:

1. detect back edge: f -> a
2. initial loop blocks: {a, f}
3. add c since it points to f, loop blocks: {a, f, c}
4. add b, e since they point to c, blocks: {a, f, c, b, e}
5. add d, since it points to e, blocks: {a, f, c, b, e, d}

alternative algorithm:

detect cycle c -> d -> e, but no edges are back edges
detect cycle a -> b -> c -> f, loop blocks: {a, b, c, f}
detect cycle a -> b -> e -> c -> f -> a, loop blocks: {a, b, e, c, f, a}

The standard identifies blocks d, the alternative does not. The cycle algorithm cannot see it because c -> d -> e doesn't have the necessary back edge and any other cycles that include d cannot escape repeating a blocks in the {c, d, e} subgraph. Its as if this subgraph is a little cycle detection trap.

This is all captured in a demo script nat_loop_vs_cycle.py.

Implementing loop detection in binaryninja has its surprises. Back edges have at least two variations in definition. The first, less strict, is an edge from an descendent to an ancestor. This is the basic_block.back_edge attribute, and ignorance of this distinction spawned an issue. By requiring the ancestor to dominate the descendent, you get the stricter version, necessary in the textbook natural loops detection algorithm:

back_edges = []
for bb in func.basic_blocks:
    for edge in bb.outgoing_edges:
        if edge.target in edge.source.dominators:
            back_edges.append(edge)

Labeling the back edge destination "header" and source "footer", the loop blocks are found by reverse bread-first traversal starting at the footer up to the header. An initial check for header must be made before the first movement, otherwise you'll miss the ending condition when header and footer are the same block, a block that branches to itself.

interpretting the algorithm's results

A result guarantees the blocks form a loop. A non-result does not mean loops don't exist.

Here red is a likely loop, but isn’t an indisputable loop (look at the blue alternative paths), so the algorithm doesn’t return it. In disease terms, it’s <100% sensitive (won’t find all loops), but 100% specific (will never misidentify a loop). In logic terms, the algorithm's true result is sufficient for a loop, but not necessary. Or, an algorithm identified loop implies a loop, but the converse is not always true.

testing: against what?

Since loop detection relies on back edges which rely on dominators, a reasonable preliminary test is to compare Binja's dominator calculation to NetworkX. Every block in every function in the x86_64 version of busybox matched.

Is there any ground truth for loop detection? I don't know of any. You can click manually through a few functions, but how do you know a problem doesn't exist in much larger functions that you can't inspect by hand? I was unable to find an existing loop discovery tool in pypi, so I wondered if the graph theory functionality provided by the NetworkX library could utilized.

And I think it's actually an advantage that comparison will be made against an algorithm that's identical, just ported to a different library.

In other words, the comparison algo_in_binja(input) == algo_in_networkx(input) does not detect if the error is in the algorithm itself, because the possible mistake exists on both sides.

I found NetworkX can return cycles with its direct .simple_cycles() function. Then I reasoned that any cycle with an edge where the destination dominates the source is a back edge, and all other blocks are members of the loop.

testing: natural loop detection vs. cycle detection

This is a pretty nice definition, and it does return loops, but in some strange cases its behavior diverges from the natural loop detection algorithm:

Loop detection algorithm behaves like:

1. detect back edge: f -> a
2. initial loop blocks: {a, f}
3. add c since it points to f, loop blocks: {a, f, c}
4. add b, e since they point to c, blocks: {a, f, c, b, e}
5. add d, since it points to e, blocks: {a, f, c, b, e, d}

Note that d is included in the loop.

Now look at how the cycle detection algorithm behaves:

detect cycle c -> d -> e, but no edges are back edges
detect cycle a -> b -> c -> f, loop blocks: {a, b, c, f}
detect cycle a -> b -> e -> c -> f -> a, loop blocks: {a, b, e, c, f, a}

Note d is not returned. The cycle algorithm cannot see it because c -> d -> e doesn't have the necessary back edge and any other cycles that include d cannot escape repeating a block in the {c, d, e} subgraph. Its as if this subgraph is a little cycle detection trap.

This is all captured in a demo script nat_loop_vs_cycle.py.

testing: on what functions?

The x86_64 version of busybox I used has 3243 functions and some really cool gnarly graphs: